如何做好資金管理，凱利公式告訴你答案

當選好想要購買的股票後，總是在煩惱要投入多少比例的資金去投資，才能賺最多錢呢?凱利公式可以告訴我們答案!!!

在說明凱利公式前，先舉個例子說明，假設今天有一個賭局，這個賭局可以進行無限次，每次下注的金額由自己決定， 今天你手上有1000元，贏了可以拿到下注金額的收益，輸了則是賠掉下注金額，要怎樣下注才能使長期收益最大化?

我們一定會先去計算這個賭博它的期望值，看它是正的還是負的，正的就值得投資，負的就不值得投資。

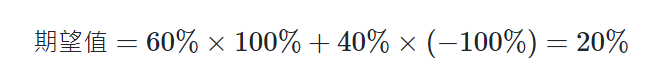
可以看到上式我們計算出來的期望值是正的，所以我們每次都投入最多的本金去獲得最大的長期收益， 但事實上投入最大的本金反而會讓你虧到什麼都不剩!!!，我們可以透過程式來模擬一下每次都投入最多的本金最終會如何?

我們按照上述設定，每次分別投入本金的30%、50%、70%、90%以及100%，開始進行模擬:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def gamble_simulator(initial_fund, run_number, win_prob):
    gs_df = pd.DataFrame({'30%':[], '50%':[], '70%':[], '90%':[], '100%':[], 'win_or_loss':[]})

    # 使用二項分布抽取隨機變數，1代表贏，0代表輸
    n, p = 1, win_prob  
    np.random.seed(66)
    sample = np.random.binomial(n, p, run_number)
    gs_df['win_or_loss'] = sample

    invest_percentage = [percentage for percentage in gs_df.columns if percentage != "win_or_loss"]

    for index, row in gs_df.iterrows():
        outcome = row['win_or_loss']

        for percentage in invest_percentage:
            percentage_name = percentage
            percentage = float(percentage.replace('%', '')) / 100
            # 一開始用初始資金算
            if index == 0:
                # 如果贏
                if outcome == 1:
                    earn_money = initial_fund * (1 + percentage)
                    gs_df.loc[index, percentage_name] = earn_money
                # 如果輸
                else:
                    earn_money = initial_fund * (1 - percentage)
                    gs_df.loc[index, percentage_name] = earn_money
            # 根據上一局的資金再次投入
            else:
                if outcome == 1:
                    earn_money = gs_df.loc[index-1, percentage_name] * (1 + percentage)
                    gs_df.loc[index, percentage_name] = earn_money
                else:
                    earn_money = gs_df.loc[index-1, percentage_name] * (1 - percentage)
                    gs_df.loc[index, percentage_name] = earn_money    
                    
    return gs_df
if __name__ == "__main__":
  initial_fund = 1000
  run_number = 10
  win_prob = 0.6
  gs_df = gamble_simulator(initial_fund, run_number, win_prob)

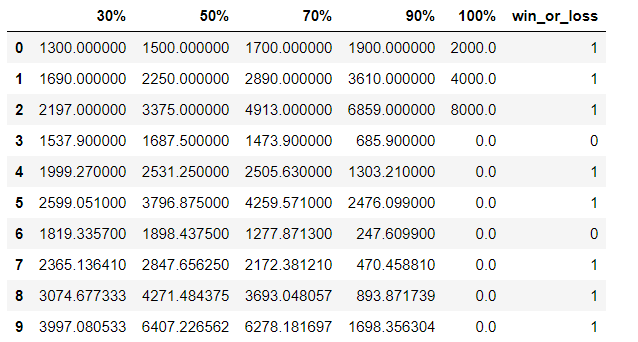
(圖一)就是我們進行十輪賭博遊戲得到的結果，可以看到如果每次都投入全部的資金，到了第四局就全部賠光光，而投入 50%以及70%則還剩6000多塊錢，30%則是剩下3997元，所以並不是投越多資金賺越多，也不是投入越少越好，因此我們需要 使用凱利公式來幫我們計算最適合投入資金的比例。

凱利公式就是為了解決這個問題而設計的，目標是使擁有正期望值的重複行為的長期增長率最大化， 公式的推導比較複雜，之後再寫一篇關於凱利公式的推導，那凱利公式如下:

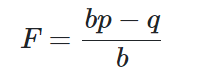
(1) b : 為賠率，也就是賺的錢 / 賠的錢

(2) p : 贏的機率

(3) q : 輸的機率

那透過程式計算可知我們每次應該要投入本金的20%來進行長期投資:

def kelly_formula(win_prob, earn_money, loss_money):
    b = earn_money / loss_money
    optimal_fund_ratio = round((b*p - (1-p)) / b, 2)
    return optimal_fund_ratio
  
if __name__ == "__main__":
  optimal_fund_ratio = kelly_formula(0.6, 100, 100)
  print('最適資金比例:%s' %(optimal_fund_ratio))

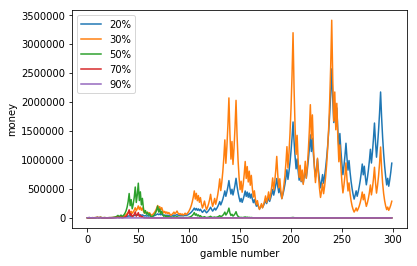
我們再次使用模擬器來看20%的本金投入的投資效益，可以看到投入比例50%、70%和90%到了第三百次的時候本金已經 接近於零，而用凱利公式算出來的最適比例20%，本金漲了好幾百倍，如果時間再拉長一點，30%的投入本金也會越來越少，所以凱利公式告訴我們，不要一次all in全部資金，應該一次投入部份的資金，分批投入賺取最大報酬率。

那以上就是關於如何進行資金管理的介紹，如果有什麼問題歡迎在下面留言，喜歡我的作品可以幫我拍拍手喔!!!