波幅統計方法 (Willbillion FB 2019-04-12 & 2019-05-01)

前言

本文轉載自筆者去年的Facebook page 兩篇有關市場波幅統計的文章, 並稍作修改:

https://www.facebook.com/willbillionquant/posts/456440908428504

https://www.facebook.com/willbillionquant/posts/467290740676854

TL; DR 概要

• 高低價格差距是量度資產品種, 尤其是指數之波幅的簡單工具.
• ATR (Average True Range) 和保力加通道寬度則是更常用的波幅統計指標.
• 年化波動率 (Annualized Volatility, "sigma") 與平方根規律則是衡量波幅時間關係的數學原理.

概念:  月份波幅統計

月份波幅分析 (Monthly Volatility Analysis) 是做指數期貨/期權過夜策略一個相當有力的工具, 雖然未必能夠完全轉變成自動化交易策略, 但結合統計觀察, 可以發現到某些非隨機漫步現象 (non random-walk behaviors), 或者從中洞察到一些高回報/風險比 (reward/risk ratio)的策略出來. 

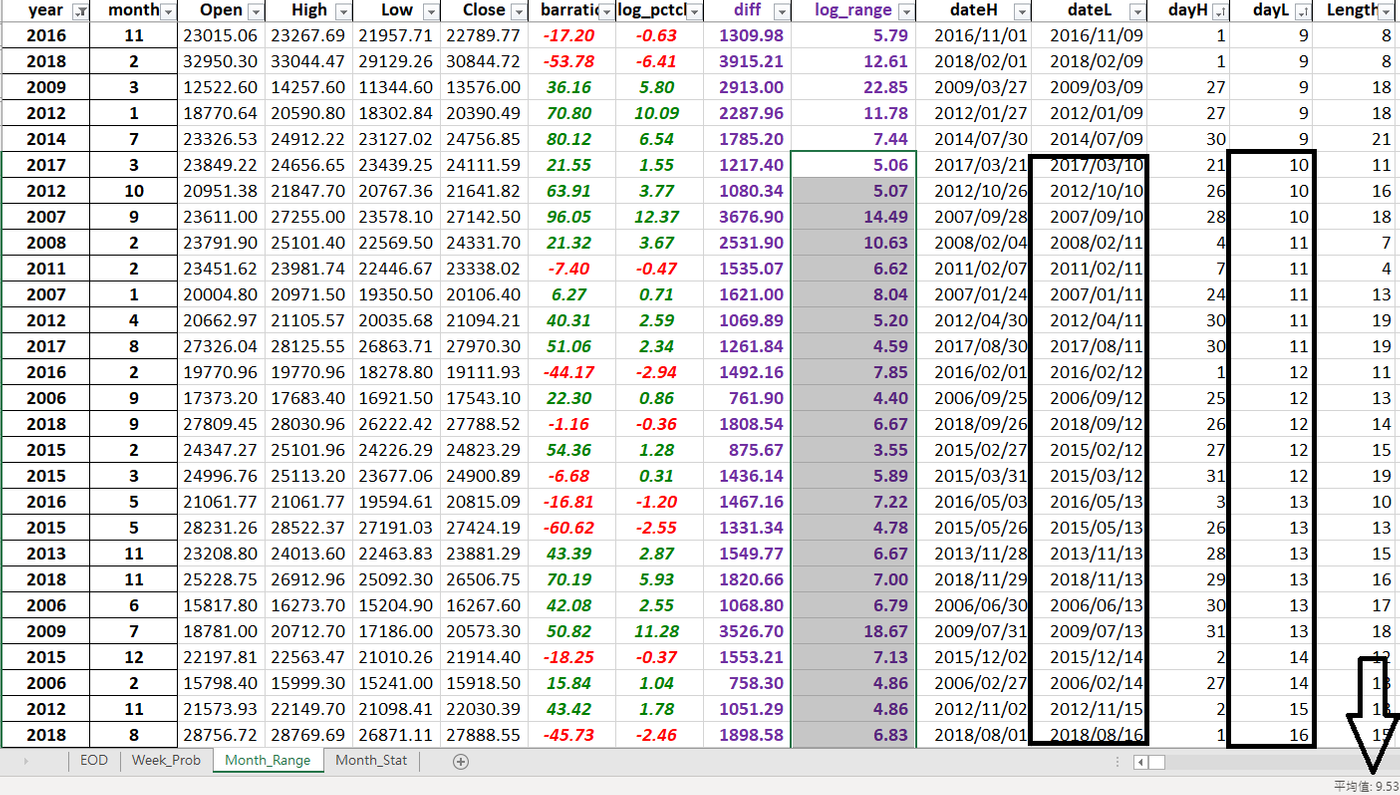
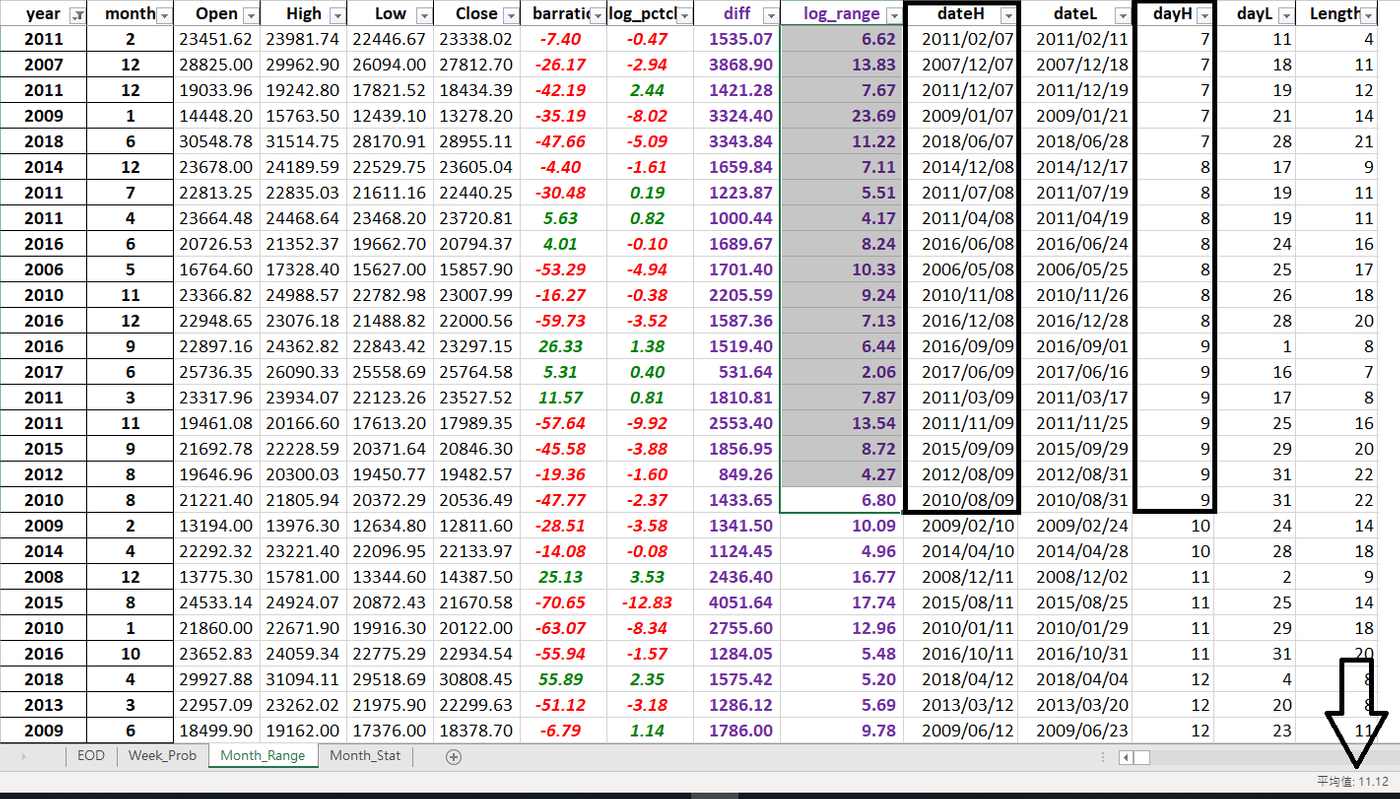
下表 Fig.1 與 Fig.2 是在下所做的2006年 – 2019年三月恆生現貨指數的月份波幅統計. 我主要關心的data field 是 本月的 自然對數波幅 (Natural logarithmic range).

插曲: 為甚麼要用 log?

筆者以前讀過初階金融數學, 金融資產價格可以視作時間序列 (time series), 而由於金融資產的變化一般會用log return 而非percentage return, 因為前者在計算average compound return來講, 具備更嚴謹的數學性質. 對於比較小的百份比變化, log return/range 大致等於 percentage return/range.

例如某月恆指波動區間為 27000 – 30000,

Log_range = ln (30000/27000) = 10.53%

percentage_range = 30000 / 27000 – 1 = 11.11%

統計結果

過去13年恆指的平均每月log range 大約是9.2%, 以現在三萬點的水平, 可以大概認為每月平均點數波幅為2500-3000點. 然後我關注每個月見當月最高位的日子(1 – 31號, 顯示在dayH一欄) 然後進行排序, 審視哪些歷史月份在頭三分之一的日子(1 – 9號)就見高位. 結果發現, 所有在1 – 9 號見高位的月份平均log range 是 11.12%, 而10 – 31號見高位的平均波幅只有8.02%.

這個觀察非常有意思. 如果是9號或之前見月內頂位, 大概可以認為之後大半個月跌市主導, 相反9號之後才見頂位, 那麼月頭就是升市主導. 從上述統計可以得到的啟發是, 跌市主導月份 (“bearish months”) 比起升市主導月份 (“bullish months”) 的波幅要大. 部署指數期權策略的話, 配合其他技術信號, 如果在1 – 9 號發出頂位沽空信號, 用long strangle 或者ratio strangle博取大波幅或偏淡策略, 勝算比起其他月份要高. 或者其他更短線的趨勢跟蹤或大波幅策略也會有更大的勝算, 配合回測後可以考慮在10 – 31 號增加此類策略的注碼.

另外如果我們是觀察每月低位的日子(dayL 一欄), 10 – 31 號見低位的月份 (都算是”跌市主導”月份) 平均波幅有9.53%, 而1 – 9號見低位月份(升市主導) 則只有8.02%, 跟用每月高位日子的觀察異曲同工.

概念: 高低平均波幅 / Average True Range

接續之前有關恆指月份波幅的探討. 這次就會結合日/周/月數據去更深入研究各品種的波幅. 找尋或開發單一資產品種的策略, 我反而會先注重研究一個品種的 歷史波動幅度 (Historical Volatility Level), 以了解策略合理的獲利幅度以及風險幅度大概是甚麼水平, 減低不合理的期望. 例如操作股票日線圖策略而言, 大藍籌股如港交所(388), 內銀, 或者美股ETF等, 最近幾年大多數每天1-3%幅度不等, 但比較波動的中小盤股隨便一天10%+ 震盪, 操作大藍籌用上5% 止蝕10%+ 止賺的幅度或許獲利甚豐, 但換上小盤股就非常容易頻繁被止蝕割肉.

第一種是高低平均幅度 (Average price range), 衡量每支bar高位減低位的平均距離. 如果計及過夜裂口的話, 就是 Average True Range (ATR) 的概念. 計算點數對於操作期貨/外匯比較好用.這類點數可以視為獲利/止蝕幅度的參考, 如果策略能夠捕捉到接近單日低位去買入的話, 一個ATR平均就會到達當日的最高位. Keltner Channel 就是平均線之上n 個ATR 跟之下n個ATR 之間的區域, 比起保力加通道 (Bollinger bands) 而言, Keltner channel 對極端波幅的出現的反應比較遲鈍.

如果是股票/ETF的話, 把ATR除以平均價格, 或者用之前文章所講的log range, 所得的就是百分比幅度 (percentage range), 例如盈富基金/恆指現貨過去十年每月幅度平均8%, 港交所(388) 過去五年每日幅度平均2%. 對於較長線的策略而言, percentage range比起ATR會更為適合.

概念: 標準差 / Bollinger Bands

第二種是價格標準差 (Standard Deviation of price, SD), 大家溫習高中數學就知道, 標準差是Variance (變異數/方差) 的平方根 (square root), 而variance 就是對比樣本均數的平均平方距離 (Average square distance from sample mean).

保力加通道 (Bollinger Bands), 例如 Bol(21, 2), 就是21天平均線(simple moving average) 之上2個SD 以及之下2個SD 的價格水平.

選擇2個SD大概是基於假設價格跟平均線的距離遵從 正態分布 (normal distribution), 根據假設有95%概率現在的價格會落在Bol(21, 2) 的裡面而不會超越上述兩個”極端價格水平”. 因此, 標準差直接跟保力加通道的寬度成正比.

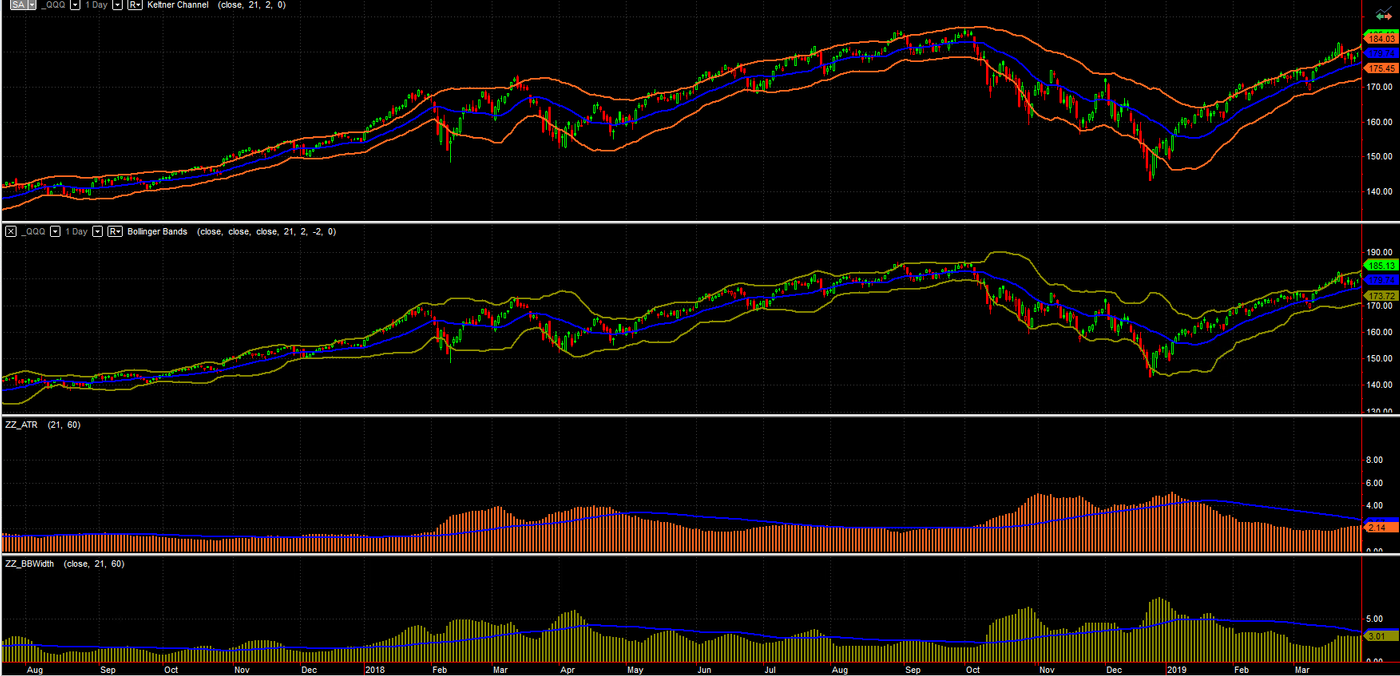
必須說明的是, 上述正態分布只是理論假設, 價格的肥尾風險 (Fat tail risk) 可以遠遠超出正態分布imply 的幅度 (特別是股災或突發消息市況). 不過標準差比起ATR, 概率意義比較明顯, 而且當極端波幅出現時, 通道的擴張也比較快, 所以我仍然喜歡運用Bollinger bands 做不少短線算法策略. 對比Fig.3 下方兩個histogram, BBWidth的變化比起ATR要急促.

概念: 年化波幅 / Sigma

第三種是 年化波動率 (Annualized volatility).

對數回報 Log return 的公式為log (price / price[1]), 比起百份比回報 (price / price[1] – 1) * 100%, 計算幾個時間段的平均複利回報會適合很多, 例如某股份第一年升了100%, 第二年下跌50%, 實際上兩年後股價回到了原位, 因此平均複利回報是零, 用log return來算就可以精確得到零, 但平均百份比回報則是(100% – 50%) / 2 = 25%, 明顯不符合實情.

假設市場為隨機漫步模型 (random walk model). log return 會遵循正態分布, 因此量度log return 的SD 就是某種波幅的衡量. 根據隨機漫步模型的數學特性, 我們要運用 “平方根定律 (law of square root)” 去把不同周期的 SD 標準化到一年的時間長度裡來衡量, 得出年化波動率, 也就是期權引申波幅裡面的sigma. 一年有12個月, 52周, 大約252個交易日, 然則

daily_sigma = sqrt(252) * SD(daily log return)

monthly_sigma = sqrt(52) * SD(monthly log return)

yearly_sigma = sqrt(12) * SD(monthly log return)

Fig.4 顯示運用63天daily log return 跟13周weekly log return (都是大約三個月的長度) 去計算sigma, 得出的讀數13.88% 與10.54% 都是屬於年化波動率的估算, 基於這個估算大概可以認為QQQ 一年內不超過11-14% 波幅的機會率約有七成 (正態分布+/- 1 個標準差), 不超過22-28%的機率則有95%.

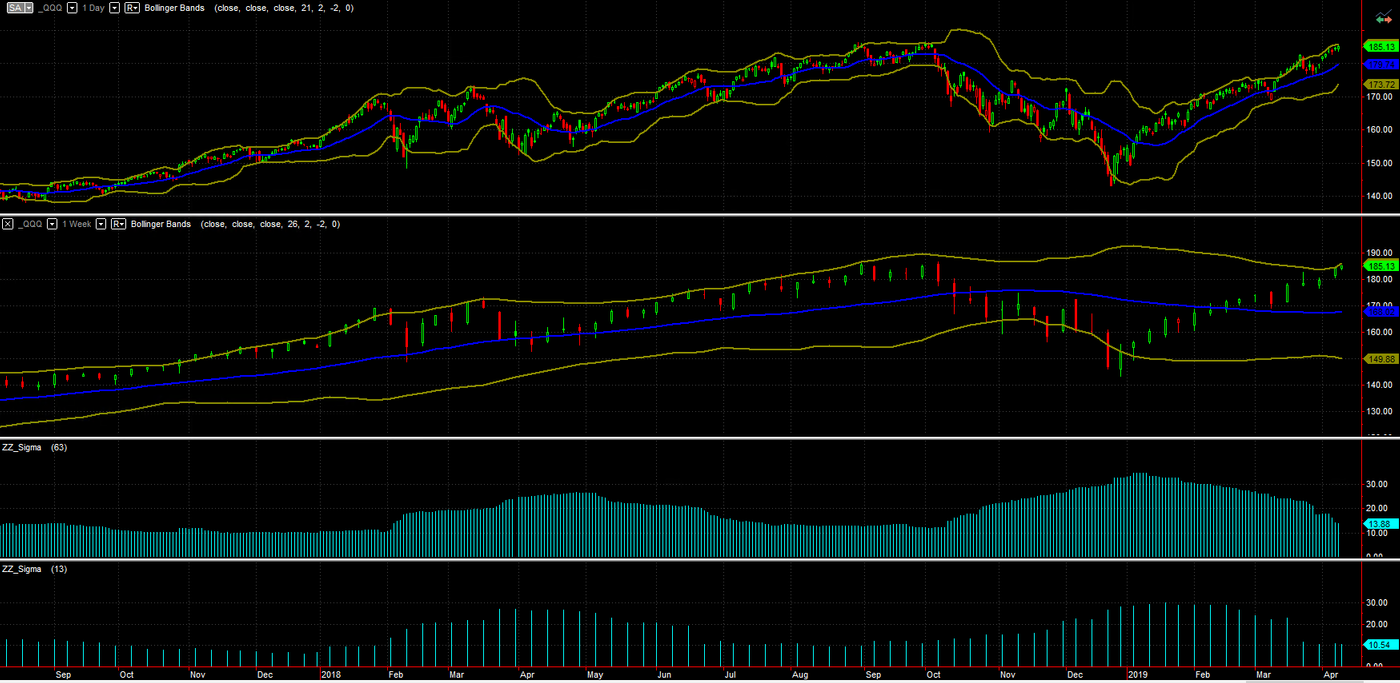
平方根定律的用途是對組合 (portfolio) 的風險限制進行估算. 以每周5個交易日, 每月21交易日而言, 如果整個投機組合單日風險不超過2%而言, 那麼在單周以內, 風險最好不超於 2% * sqrt(5) = 4.5%, 而單月以內風險暴露不超過 2% * sqrt(21) = 9.2% 或者10%.

結論

小小的結論是, 波幅統計基本算是測量每個品種的”脈搏”, 如此重要的東西, 小弟已經用python program 為自己監察的各類品種每天自動計算並且update波幅統計. 當然大家也可以基於上述idea去構思更加深入的波幅統計喔~~~